DERIVADAS Y SUS APLICACIONES
Derivada de una función en un punto
Dada una función real, y = f(x), se define la derivada de la función en el punto x = a. Se representa por f´(a) y se calcula como:
Es importante tener en cuenta que:
- La derivada de una función en un punto es un número real, que puede ser positivo, negativo o cero
- La derivada de la función en un punto es la pendiente de la recta tangente que pasa por el punto (a, f(a))
Función derivada
Dada una función real, y = f(x), se define la función derivada de f, o simplemente la derivada de f, a una función que asocia a cada valor de x con la derivada en ese punto. Se representa por f´(x) o y´y se calcula como:
Con este applet de Geogebra podrás entender el significado de la derivada de una función en un punto y la obtención de la función derivada. Para ello basta con escribir la expresión algebraica de la función cuya derivada quieras estudiar y pulsar INTRO: aparecerá automáticamente la gráfica de dicha función.
Para escribir las funciones correctamente debes saber que:
1.- Los símbolos utilizados en las operaciones básicas son: suma (+); resta (-); producto (*); cociente (/); potencia (^), todos ellos en el teclado del ordenador
2.- Las funciones radicales hay que escribirlas como potencias de exponente fraccionario
3.- Las funciones trigonométricas se escriben: seno: sin(f); coseno: cos(f); tangente: tan(f)
4.- En las funciones racionales, tanto el numerador como el denominador deben estar escritas entre paréntesis
5.- Las funciones logarítmicas se escriben: logaritmos neperianos: ln(f); logaritmos decimales: log(10,f); logarirmos en base a: log(a,f)
Desplaza el punto P con la casilla "Ver derivada en cada punto" activada y fíjate en la valor de la derivada en ese punto (representado por el segmento verde)Al activar el rastro de la función derivada podrás observar la representación de la función derivada a medida que desplazas el punto, que coincide con la gráfica que se obtiene al activar "Función derivada"
Utiliza los iconos de la parte superior para mover, hacer más grande o más pequeña la representación
Derivada de funciones elementales
Las reglas de derivación permiten calcular las funciones derivadas sin necesidad de calcular el límite
Derivada de operaciones de funciones
Con estas técnicas de derivación se pueden obtener las funciones derivadas de cualquier operación de funciones
Con este applet de Geogebra podrás comprobar si calculas y simplificas bien las derivadas.
Para ello basta con escribir la expresión algebraica de la función cuya derivada quieras calcular y pulsar INTRO: aparecerá automáticamente la función derivada
Las instrucciones para escribir las funciones, son las mismas que en el applet anterior
Derivadas sucesivas
Dada una función, y = f(x), a partir de su derivada, y´, podríamos calcular nuevamente la derivada, es decir, estaríamos calculando la derivada de la derivada, también llamada segunda derivada, y´´, y así sucesivamente.
Derivabilidad de una función en un punto
Una función, y = f(x), es derivable en un punto x = a, si:
En el caso de funciones definidas a trozos, para concluir que existe la derivada en el punto hay que calcular las derivadas laterales:
Monotonía y extremos relativos
La relación que existe entre la monotonía y extremos relativos y la derivada de una función es la siguiente:
- Si la derivada es positiva la función es creciente, ya que si la función crece, las rectas tangentes son siempre crecientes y, por lo tanto, la pendiente es positiva
la función es creciente, ya que si la función crece, las rectas tangentes son siempre crecientes y, por lo tanto, la pendiente es positiva
 la función es creciente, ya que si la función crece, las rectas tangentes son siempre crecientes y, por lo tanto, la pendiente es positiva
la función es creciente, ya que si la función crece, las rectas tangentes son siempre crecientes y, por lo tanto, la pendiente es positiva
- Si la derivada se anula la función presenta un extremo relativo, ya que en estos puntos la recta tangente siempre es horizontal y, por lo tanto, la pendiente vale cero
la función presenta un extremo relativo, ya que en estos puntos la recta tangente siempre es horizontal y, por lo tanto, la pendiente vale cero
 la función presenta un extremo relativo, ya que en estos puntos la recta tangente siempre es horizontal y, por lo tanto, la pendiente vale cero
la función presenta un extremo relativo, ya que en estos puntos la recta tangente siempre es horizontal y, por lo tanto, la pendiente vale cero
- Si la derivada es negativa la función es decreciente, ya que si la función decrece, las rectas tangentes son siempre decrecientes y, por lo tanto, la pendiente negativa.
la función es decreciente, ya que si la función decrece, las rectas tangentes son siempre decrecientes y, por lo tanto, la pendiente negativa.
 la función es decreciente, ya que si la función decrece, las rectas tangentes son siempre decrecientes y, por lo tanto, la pendiente negativa.
la función es decreciente, ya que si la función decrece, las rectas tangentes son siempre decrecientes y, por lo tanto, la pendiente negativa.
Para estudiar la monotonía y extremos relativos de una función no tienes más que estudiar el signo de la derivada, tal y como se indica en el apartado "Cálculo de las propiedades" dentro de este mismo blog
Curvatura y puntos de inflexión
La relación que existe entre la curvatura y los puntos de inflexión y la segunda derivada de una función es la siguiente:
- Si la segunda derivada es positiva la función es convexa, ya que si dibujamos las rectas tangentes, las pendientes van creciendo y, por lo visto anteriormente, si la derivada va creciendo implica que la segunda derivada es positiva
la función es convexa, ya que si dibujamos las rectas tangentes, las pendientes van creciendo y, por lo visto anteriormente, si la derivada va creciendo implica que la segunda derivada es positiva
 la función es convexa, ya que si dibujamos las rectas tangentes, las pendientes van creciendo y, por lo visto anteriormente, si la derivada va creciendo implica que la segunda derivada es positiva
la función es convexa, ya que si dibujamos las rectas tangentes, las pendientes van creciendo y, por lo visto anteriormente, si la derivada va creciendo implica que la segunda derivada es positiva
- Si la segunda derivada se anula la función presenta un punto de inflexión, ya que hay un cambio en la curvatura y, por lo tanto, un cambio en el signo de la segunda derivada, teniendo que pasar por cero
la función presenta un punto de inflexión, ya que hay un cambio en la curvatura y, por lo tanto, un cambio en el signo de la segunda derivada, teniendo que pasar por cero
 la función presenta un punto de inflexión, ya que hay un cambio en la curvatura y, por lo tanto, un cambio en el signo de la segunda derivada, teniendo que pasar por cero
la función presenta un punto de inflexión, ya que hay un cambio en la curvatura y, por lo tanto, un cambio en el signo de la segunda derivada, teniendo que pasar por cero
- Si la segunda derivada es negativa la función es cóncava, ya que si dibujamos las rectas tangentes, las pendientes van decreciendo y, por lo visto anteriormente, si la derivada va decreciendo implica que la segunda derivada es negativa
la función es cóncava, ya que si dibujamos las rectas tangentes, las pendientes van decreciendo y, por lo visto anteriormente, si la derivada va decreciendo implica que la segunda derivada es negativa
 la función es cóncava, ya que si dibujamos las rectas tangentes, las pendientes van decreciendo y, por lo visto anteriormente, si la derivada va decreciendo implica que la segunda derivada es negativa
la función es cóncava, ya que si dibujamos las rectas tangentes, las pendientes van decreciendo y, por lo visto anteriormente, si la derivada va decreciendo implica que la segunda derivada es negativa
Para estudiar la curvatura y puntos de inflexión de una función no tienes más que estudiar el signo de la segunda derivada, tal y como se indica en el apartado "Cálculo de las propiedades" dentro de este mismo blog
Recta tangente
Como la derivada de la función en un punto representa la pendiente de la recta tangente en dicho punto, para hallar la ecuación de la recta tangente en el punto de coordenadas (a, f(a)) podemos utilizar la ecuación punto-pendiente:
Optimización de funciones
Optimizar una función es encontrar sus extremos relativos bajo ciertas condiciones determinadas por relaciones funcionales.
Hay muchos ejemplos en la ciencia, tecnología, economía, finanzas, demografía y medicina que responden a un problema de optimización: buscar un envase que tenga la mayor capacidad con la menor superficie posible, invertir una cierta cantidad de dinero para obtener el máximo beneficio posible sujeto a ciertas condiciones de riesgo, etc.
Para resolver un problema de optimización, se sigue este procedimiento:
- Se escribe la función que se desea optimizar y las condiciones del problema, si las hubiere, en forma de ecuaciones que relacionan las variables y los datos
- Si la función depende de dos variables, se utilizan las ecuaciones para expresarla en función de una única variable
- Se calculan los extremos relativos de la función derivando, identificando los máximos y los mínimos mediante la monotonía
- Se interpretan los resultados y se rechazan aquellos que no sean posible, bien por las condiciones o por la naturaleza del problema







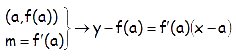
Comentarios
Publicar un comentario